HUKUM KIRCHHOFF

HUKUM KIRCHHOFF adalah dua persamaan yang berhubungan dengan arus dan beda potensial (umumnya dikenal dengan tegangan) dalam rangkaian listrik. Hukum ini pertama kali diperkenalkan oleh seorang ahli fisika Jerman yang bernama Gustav Robert Kirchhoff (1824-1887) pada tahun 1845.

Gambar 1.1 merupakan contoh rangkaian dari hukum kirchhoff.
Tegangan jatuh pada  dan  tidaklah sama karena adanya ggl . Sehingga, rangkaian kedua resistor ini tidaklah paralel juga bukanlah rangkaian seri, karena arus yang mengalir pada kedua resistor tidaklah sama. Namun, ada hukum yang berlaku pada rangkaian yang memliki arus tetap (tunak). Hukum ini adalah hukum Kirchhoff 1 dan 2.

Hukum Kirchhoff 1

dikenal sebagai hukum percabangan (junction rule), karena hukum ini memenuhi kekekalan muatan. Hukum ini diperlukan untuk rangkaian yang multisimpal yang mengandung titik-titik percabangan ketika arus mulai terbagi. Pada keadaan tunak, tidak ada akumulasi muatan listrik pada setiap titik dalam rangkaian. Dengan demikian, jumlah muatan yang masuk di dalam setiap titik akan meninggalkan titik tersebut dengan jumlah yang sama.

Hukum Kirchhoff 1 menyatakan bahwa:

“Jumlah arus listrik yang masuk melalui titik percabangan dalam suatu rangkaian listrik sama dengan jumlah arus yang keluar melalui titik percabangan tersebut”

Ilustrasi hukum Kirchhoff tentang titik percabangan. Arus I_1yang mengalir melalui titik percabangan a akan sama dengan jumlah I_2+I_3 yang keluar dari tiik percabangan

Secara umum rumus hukum Kirchhoff 1 dapat dituliskan sebagai berikut:

Gambar 1.2 menunjukkan suatu titik percabangan dari 5 buah kawat yang dialiri arus  dan .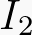

Dalam rentang waktu , muatan 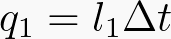 mengalir melalui titik percabangan dari arah kiri. Dalam rentang waktu  juga, muatan  dan  bergerak ke arah kanan meninggalkan titik percabangan. Karena muatan tersebut bukan berasal dari titik percabangan dan tidak juga menumpuk pada titik tersebut dalam keadaan tunak, maka muatan akan terkonservasi di titik percabangan tersebut, yaitu:

Hukum Kirchhoff 2

“Pada setiap rangkaian tertutup, jumlah beda potensialnya harus sama dengan nol”

Hukum Kirchhoff 2 juga sering disebut sebagai hukum simpal (loop rule), karena pada kenyataannya beda potensial diantara dua titik percabangan dalam satu rangkaian pada keadaan tunak adalah konstan. Hukum ini merupakan bukti dari adanya hukum konservasi energi. Jika kita memiliki suatu muatan Q pada sembarang titik dengan potensial V, dengan demikian energi yang dimiliki oleh muatan tersebut adalah QV. Selanjutnya, jika muatan mulai bergerak melintasi simpal tersebut, maka muatan yang kita miliki akan mendapatkan tambahan energi atau kehilangan sebagian energinya saat melalu resistor baterai atau elemen lainnya. Namun saat kebali ke titik awalnya, energinya akan kembali menjadi QV.

Sebagai contoh penggunaan hukum ini (Gambar 1.3), dua baterai yang berisi hambatan dalam  dan  serta ada 3 hambatan luar. Kita akan bisa menenutukan arus dalam rangkaian tersebut sebagai fungsi GGL dan hambatan.

Rangkaian berisi 2 buah baterai dan 3 resistor eksternal. Tanda plus minus pada resistor digunakan untuk mengingatkan kita sisi mana pada setiap resistor yang berada pada potensial lebih tinggi untuk arah arus yang diasumsikan.

Secara umum rumus hukum Kirchhoff 2 dapat dinyatakan sebagai berikut: Sigma 1 Masuk Sigma 2 Keluar
Sumber :https://www.studiobelajar.com/hukum-kirchhoff/